У меня тоже есть одна претензия. К вот этому.
Цитата:
Теорема о параллельных прямых.
Если внутренние накрест лежащие углы равны, то прямые параллельны
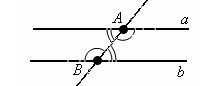
Доказательство.
Пусть прямые a и b образуют с секущей AB равные внутренние накрест лежащие углы.
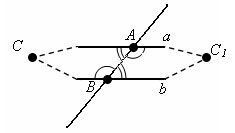
Допустим, прямые a и b не параллельны, а значит, пересекаются в некоторой точке С.
Отложим от секущей AB треугольник ABC1, равный треугольнику ABC, так, что вершина С1 лежит в другой полуплоскости, чем вершина С.
По условию внутренние накрест лежащие углы при параллельных прямых a, b и секущей AB равны.
Из равенства треугольников следует, что ∠ CAB = ∠ C1BA и ∠ CBA = ∠ C1AB и они совпадают с внутренними накрест лежащими углами. Значит, прямая AC1 совпадает с прямой a, a прямая BC1 совпадает c прямой b. Отсюда следует, что через две различные точки С и С1 проходят две различны прямые a и b. Это противоречит аксиоме о том, что «Через любые две точки можно провести прямую, и только одну». Значит, прямые параллельны.
|
Нафиг, к чертям. Если прямые пересекаются, то они не параллельные, а если не пересекаются - параллельны. Всё. Доказательство следует из определения.